[WEEK01] 8/15 TIL_힙 정렬
선택 정렬을 응용한 알고리즘인 힙 정렬을 알아보겠다. 힙 정렬은 힙의 특성을 이용하여 정렬하는 알고리즘이다. 힙은 부모의 값이 자식의 값보다 항상 크다는 조건을 만족하는 완전 이진트리이다.
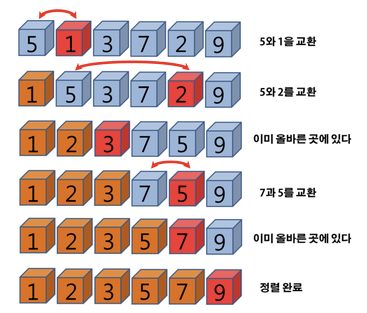
선택 정렬
먼저 힙 정렬에 알아보기 전에 선택 정렬을 알아보자. 선택 정렬은 '가장 작은 원소부터 정렬하는 방법'이다.
힙 정렬 - 특성
힙(heap) 정렬은 힙의 특성을 이용하여 정렬하는 알고리즘이다. 힙은 '부모의 값이 자식의 값보다 항상 크다'는 조건을 만족하는 완전 이진 트리이다. 이때 부모의 값이 자식의 값보다 항상 작아도 힙이라고 한다. 힙(heap)은 쌓아 놓음을 의미한다.
트리의 가장 윗부분에 위치한 노드를 루트(root)라고 하고 가장 하래에 위치한 노드를 리프(leaf)라고 한다.

힙은 최대 힙과 최소 힙이 있다.

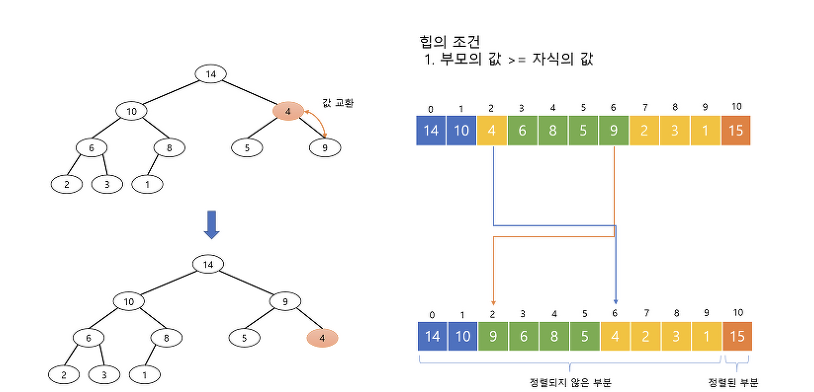
하기 그림은 힙의 원소를 배열에 어떻게 저장할 것인지를 나타낸다. 가장 위쪽에 있는 루트(15)를 a[0]에 저장한다. 그리고 한 단계 아래 왼쪽 원소(10)에서 오른쪽 원소(14)로 따라 간다. 이 과정에서 배열의 인덱스값을 1씩 증가시키며 각 원소를 저장한다.
이 작업을 가장 마지막에 있는 원소(4)까지 반복하여 힙을 배열에 저장하면 완료된다.

이러한 순서로 힙을 배열에 저장하면 부모 인덱스와 왼쪽 아래에 있는 자식(왼쪽 자식), 오른쪽 아래에 있는 자식(오른쪽 자식) 인덱스 사이에는 다음과 같은 관계가 성립한다.
원소 a[i]에서
- 부모: a[(i -1 ) // 2]
- 왼쪽 자식: a[i*2 + 1]
- 오른쪽 자식: a[i*2 + 2]
힙 정렬 - 알고리즘
힙 정렬의 알고리즘은 다음과 같다.
- 힙에서 최댓값인 루트를 꺼내 맨 끝 원소와 교환한다.
- 루트 이외의 부분을 힙으로 만든다.
이를 구체적으로 알아보자.

이 순서대로 힙 정렬을 수행한다. 이때 중요한 것은 배열의 처음 상태가 힙의 요구 사항을 만족하지 않을 수 있다는 것이다. 따라서 이 순서를 적용하기 전에 배열을 반드시 힙으로 만들어야 한다.
힙 정렬 - 배열을 힙으로 만들기
배열을 힙으로 만드는 방법 중 하나인 상향식(bottom-up) 방법은 가장 아랫부분의 오른쪽 서브트리부터 힙을 만들고, 같은 단계에 있는 왼쪽 서브트리로 진행한다. 그 단계를 완료하면 한 단계 위로 이동하면서 각각의 서브트리를 힙으로 만든다.

힙 정렬 - 코드
from typing import MutableSequence
# 원소 수가 n인 배열 a를 힙 정렬하는 함수이다.
def heap_sort(a: MutableSequence) -> None:
# 배열 a에서 a[left] ~ a[right] 원소를 힙으로 만든다 a[left] 이외에는 모두 힙 상태라고
# 가정하고 a[left]를 아랫부분의 알맞은 위치로 옮겨 힙 상태를 만든다
def down_heap(a: MutableSequence, left: int, right: int) -> None:
# left 부모 노드를 기준으로 하위 노드를 모드 heapify 함. right는 마지막 노드의 index
temp = a[left] # 부모 노드의 값을 temp에 저장. 이후 저 큰 자식 값이 없으면 계속 내려감
parent = left # 부모 노드 index 지정
while parent < (right + 1) // 2: # 부모 노드의 최대 index +1해줌. 가장 마지막 노드+1 // 2
cl = parent * 2 + 1 # 왼쪽 노드 index
cr = cl + 1 # 오른쪽 노드 index
child = cr if cr <= right and a[cr] > a[cl] else cl
# 큰 값을 선택 + cl = right 가장 마지막 노드가 되면 cr의 값이 존재 하지 않아 범위를 벗어남.
if temp >= a[child]: # 부모 값이 자식보다 크면
break # 멈춤
a[parent] = a[child] # 자식 값이 더 크면 자식 값을 부모 값에 대입
parent = child # 기준 index를 자식 level로 내려감
a[parent] = temp # 끝까지 다 내려갔으면 처음 tmp에 저장했던 부모 노드 값을 leaf에 대입
n = len(a)
# down_heap() 함수를 호출하여 배열 a를 힙으로 만든다.
for i in range((n - 1) // 2, -1, -1): # 가장 마지막 부모 노드부터 시작. 상향식 heapify
down_heap(a, i, n-1)
# 최댓값인 루트 a[0]을 꺼내 배열의 마지막 원소와 교환하고, 배열의 남은 부분을 다시 힘으로 만드는
# 과정을 반복하여 정렬을 수행한다.
for i in range(n - 1, 0 ,-1):
a[0], a[i] = a[i], a[0] # root값을 마지막 leaf 노드 가장 오른쪽에 저장
down_heap(a, 0, i - 1) # 옮겨진 root값을 제외하고 다시 heapify
if __name__=='__main__':
num = int(input())
x = [int(x) for x in input().split()]
print(heap_sort(x))
'정글 2기 > 알고리즘' 카테고리의 다른 글
| [WEEK03] 알고리즘_그래프, DFS, BFS (0) | 2021.08.20 |
|---|---|
| [백준_11279] 우선순위 큐, 최대 힙 (0) | 2021.08.16 |
| [백준_2470] 중, 이분 탐색, 두 용액 (0) | 2021.08.13 |
| [백준_2110] 중, 이분 탐색, 공유기 설치 (0) | 2021.08.13 |
| [백준_2805] 하, 이분 탐색, 수 찾기 (0) | 2021.08.12 |




댓글