[C언어] 레드-블랙 트리(Red-black Tree, RB Tree)
트리 구조 중 가장 복잡한 구조인 레드-블랙 트리에 대해 배워보자. RBT는 자가 균형 이진 탐색 트리로서 실 사용에서 효율적이고 최악의 경우에도 상당히 우수한 실행 시간을 보인다. 트리에 n개의 원소가 있을 때 O(log n)의 시간복잡도로 삽입, 삭제, 검색을 할 수 있다.
Red-black tree 의 특징
RBT의 특징
- 모든 노드는 빨강이거나 검정이다.
- 루트는 검정이다. (검정으로 변환)
- 모든 리프(NIL)는 검정이다.
- 노드가 빨간색이면 그 노드의 자식은 모두 검정이다. (연속 빨간 노드는 회전 필요)
- 각 노드로부터 그 노드의 자손인 리프로 가는 경로들은 모두 같은 수의 검정 노드를 포함한다.
- 부모노드는 왼쪽 서브트리보다 크고 오른쪽 서브트리보다 작다.
- 새로 삽입되는 노드는 Leaf에 위치하며 빨간 노드이다.
- 부모의 두 자식노드가 모두 빨간 노드이면, 부모를 빨간 노드로 하고 자식은 검정 노드로 바뀔 수 있다.(색상변환)
- 빨간 노드는 자식이 없던가, 있다면 두개의 검정 노드여야 한다.
- 검정 노드는 자식이 없던가, 있다면 하나의 빨간 노드나 두개의 빨간 노드나 두개의 검정 노드를 가진다. - 하나의 검정 노드 X
RBT의 기본 동작
레드-블랙 트리의 읽기 전용 동작(탐색)은 이진 탐색 트리의 읽기 전용 동작과 동일한 방식으로 구현해도 된다. 이는 레드-블랙 트리가 이진 탐색 트리의 특수한 형태이기 때문이다. 하지만 레드-블랙 트리의 특성을 유지하기 위해 O(log n) 또는 amortized O(1)번의 색변환과 최대 3회 (삽입은 최대 2회)의 트리 회전을 필요로 한다. 하지만 여전히 복잡도는 O(log n)이다.
1. 색변환(Color Flip)
- 상향 색변환 (B-Tree의 Split 동작)
- 부모의 두 자식노드가 모두 빨간 노드이면, 부모를 빨간 노드로 하고, 자식은 검정 노드로 바꿀 수 있다. (부모가 검정색 루트인 경우 예외)
- 하향 색변환 (B-Tree의 BindNode 동작) - 삭제를 위해 사용됨
- 부모가 빨간 노드이면, 자신을 검정 노드로 하고 자식들을 빨간 노드로 바꿀 수 있다.
2. 회전(Rotation)
- 이진트리의 규칙을 깨지 않고 트리를 재구성하는 방법
- 우회전(Right Rotation)과 좌회전(Left Rotation)
- 좌우의 트리 높이를 맞추는 방향으로 회전 ( AVL 트리의 기본 Operation)

3. 삽입
레드-블랙 트리의 삽입은 단순 이진 탐색 트리에서 하는 것과 같이 노드를 삽입하고 색은 레드로 정하는 것을 기본으로 한다. 그 다음은 주위 노드 색상에 따라 달라진다. 이 때, 삼촌 노드(Uncle)의 개념을 도입한다.
- N : 삽입하는 원소
- P : N의 부모 노드
- G : P의 부모 노드
- U : N의 삼촌 노드
struct node *grandparent(struct node *n)
{
if ((n != NULL) && (n->parent != NULL))
return n->parent->parent;
else
return NULL;
}
struct node *uncle(struct node *n)
{
struct node *g = grandparent(n);
if (g == NULL)
return NULL; // No grandparent means no uncle
if (n->parent == g->left)
return g->right;
else
return g->left;
}
(1) N이 트리의 시작(root)에 위치하는 경우
첫 번째 속성을 만족하기 위해 N을 검은색으로 변경한다.. 이 때, 모든 경로에 블랙 노드가 추가되어 다섯 번째 속성은 유효하다.
void insert_case1(struct node *n)
{
if (n->parent == NULL)
n->color = BLACK;
else
insert_case2(n);
}
(2) N의 부모 노드 P가 블랙 노드인 경우
네 번째 속성은 유지되며 다섯 번째 속성 또한 N이 기본으로 레드이기 때문에 유효하다. 이 때, N은 할아버지 노드 G를 가지고 있다고 가정할 수 있다.
void insert_case2(struct node *n)
{
if (n->parent->color == BLACK)
return; /* Tree is still valid */
else
insert_case3(n);
}
부모 노드가 레드 노드인 경우
삽입시 4번 째 규칙 '빨간 노드의 자식들은 모두 검은색'이 위반될 수 있다.
삽입되는 노드는 항상 Red인데, 부모 노드 역시 Red이면 위반이다. 이 경우 3가지 케이스가 존재한다.
부모 노드가 레드 노드일 때,
1) 삼촌노드가 RED인 경우
2) 삼촌은 검은색, 새로 삽인한 노드가 부모노드의 오른쪽 자식인 경우
3) 삼촌은 검은색, 새로 삽인한 노드가 부모노드의 왼쪽 자식인 경우
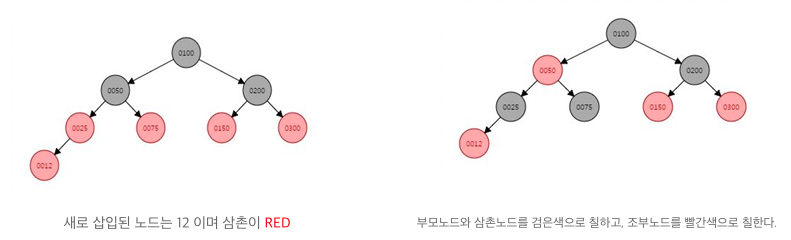
(3) N의 부모 노드 P와 삼촌 노드 U가 모두 레드 노드인 경우
네 번째 속성에 따라 부모 노드 P를 블랙 노드로 전환해야 하며 이 때, 다섯 번째 속성을 유지하기 위해 부모노드 P와 삼촌 노드 U 모두를 블랙으로 바꾸고 할아버지 노드 G를 붉은색 노드로 변경한다. 이렇게 함으로써 레드 노드인 N은 블랙 노드를 부모 노드로 가지게 된다. 그러나 이 때, 할아버지 노드 G가 두 번째 속성과 네 번째 속성을 만족하지 않을 수 있다.
- 두 번째 속성 : 루트 노드는 블랙이다.
- 네 번째 속성 : 레드 노드의 자식 노드들은 모두 블랙이다.
이를 해결하기 위해 할아버지 노드 G에 대해 지금까지 고려한 경우의 수를 재귀적으로 적용한다. 이는 삽입 과정 중에 발생하는 유일한 재귀 호출이며, 회전 작업을 하기 전에 적용해야 한다.
void insert_case3(struct node *n)
{
struct node *u = uncle(n);
struct node *g;
if ((u != NULL) && (u->color == RED)) {
n->parent->color = BLACK;
u->color = BLACK;
g = grandparent(n);
g->color = RED;
insert_case1(g);
} else {
insert_case4(n);
}
}
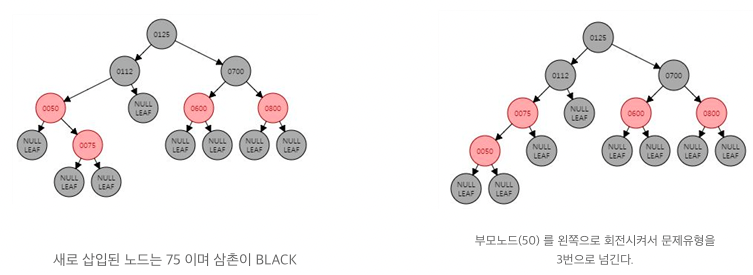
(4) N의 부모 노드 P가 레드 노드이고 삼촌 노드 U는 블랙 노드이다. 동시에 N은 P의 오른쪽 자식, P는 G의 왼쪽 자식인 경우
부모노드를 왼쪽으로 회전시켜 문제를 (5) 번 케이스로 바꾼다. N과 P 모두 레드 노드이기 때문에 회전하여도 다섯 번째 속성에 위배되지 않는다.
void insert_case4(struct node *n)
{
struct node *g = grandparent(n);
if ((n == n->parent->right) && (n->parent == g->left)) {
rotate_left(n->parent);
n = n->left;
} else if ((n == n->parent->left) && (n->parent == g->right)) {
rotate_right(n->parent);
n = n->right;
}
insert_case5(n);
}static void rotate_left(struct node *n)
{
struct node *c = n->right;
struct node *p = n->parent;
if (c->left != NULL)
c->left->parent = n;
n->right = c->left;
n->parent = c;
c->left = n;
c->parent = p;
if (p != NULL) {
if (p->left == n)
p->left = c;
else
p->right = c;
}
}
static void rotate_right(struct node *n)
{
struct node *c = n->left;
struct node *p = n->parent;
if (c->right != NULL)
c->right->parent = n;
n->left = c->right;
n->parent = c;
c->right = n;
c->parent = p;
if (p != NULL) {
if (p->right == n)
p->right = c;
else
p->left = c;
}
}
(5) N의 부모 노드 P가 레드 노드이고, 삼촌 노드 U는 블랙 노드이다. 동시에 N은 P의 왼쪽 자식, P는 G의 왼쪽 자식인 경우
부모노드를 검은색, 조부노드를 빨간색으로 칠한다. 그 다음 조부노드를 오른쪽으로 회전시킨다.

void insert_case5(struct node *n)
{
struct node *g = grandparent(n);
n->parent->color = BLACK;
g->color = RED;
if (n == n->parent->left)
rotate_right(g);
else
rotate_left(g);
}
4. 삭제
이진 탐색 트리에서 두 개의 자식 노드를 가진 노드를 지울 때, 우리는 노드의 왼쪽 서브트리에서 최댓값(predecessor)을 찾거나, 오른쪽 서브트리에서 최솟값(successor)을 찾아 해당 값을 지우고자 하는 노드로 옮긴다. 이 때, 최댓값 또는 최솟값에 해당하는 노드는 반드시 한 개 이하의 자식 노드만 가질 수 있다. 따라서 우리는 삭제에 있어서 최대 한 개의 자식을 가지고 있는 노드를 삭제하는 문제로 치환할 수 있다.
- 기본적으로 이진탐색트리의 삭제에 기반한다.
- 삭제되는 노드의 자식이 2개일 경우 successor나 predecessor로 삭제 노드를 바꿔 결국 자식이 0개나 1개인 경우로 치환
- M : 삭제하는 원소
- C : M이 한 개의 non-leaf 자식을 가질 경우 해당 노드를 C라고 하며, 그렇지 않으면 두 leaf 자식 중 아무 노드를 의미
간단한 케이스 1 : 삭제하려는 원소 M이 레드 노드인 경우,
그냥 삭제하면 된다.
간단한 케이스 2 : 삭제하려는 원소 M이 블랙 노드이고, C가 레드 노드인 경우
M을 삭제하고 C를 블랙 노드로 전환하여 붙이면 된다.
나머지 복잡한 케이스 : 삭제하는 원소 M이 블랙 노드이고, C도 블랙 노드인 경우
이중 흑색 노드 : 삭제 노드, 대체 노드가 모두 Black인 경우 삭제 후 이중 흑색 노드가 된다. 즉 흑색이 하나 적은 상태이다.
이 때 중요한 것은 이중 흑색 노드와 그 주변 노드들의 색이다.(형제, 형제의 자식, 부모 등)
복잡한 케이스 3 : 이중 흑색 노드 형제가 red인 경우
- -> 형제를 Black, 부모를 Red로 변환후 부모노드 기준으로 좌회전한다.
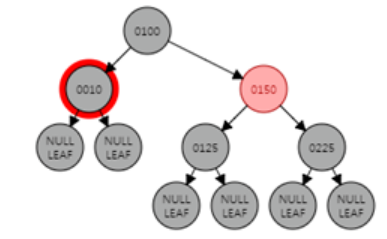


복잡한 케이스 4 : case a, b, c는 이중흑색노드의 형제가 모두 Black인 경우이다.
복잡한 케이스 4-a : 이중흑색노드의 형제가 Black이고 형제의 양쪽 자식 모두 Black인 경우
-> 형제노드만 Red로 만들고 이중흑색노드의 검은색 1개를 부모에게 전달한다. 이후 재귀적으로 root 노드까지 확인한다.
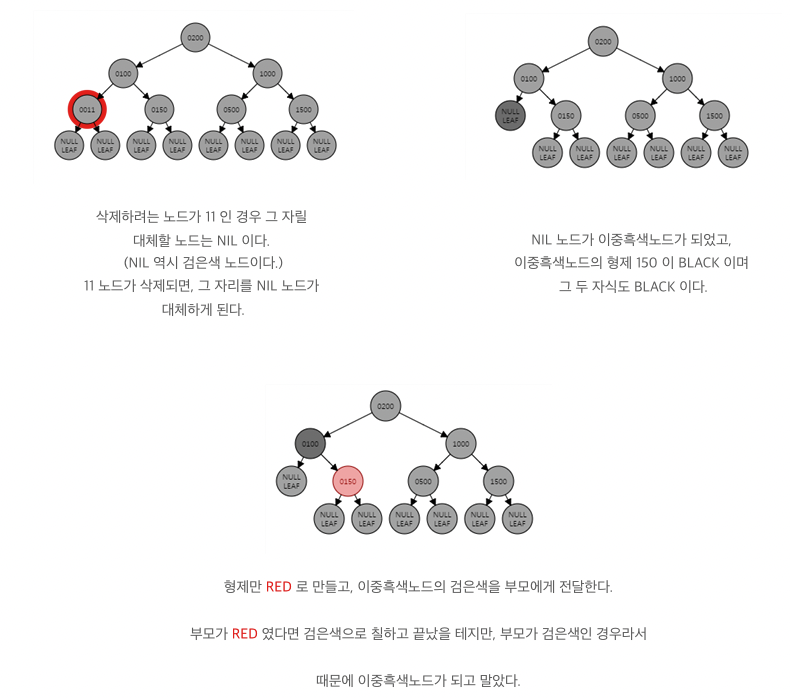
그 다음 재귀적으로 root 까지 확인
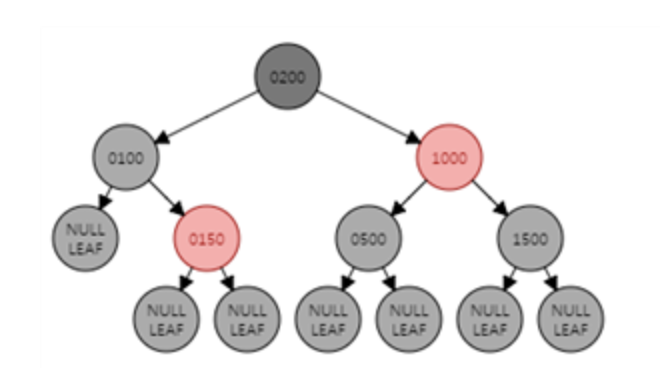
복잡한 케이스 4-b : 이중흑색노드의 형제가 Black이고 형제의 왼쪽 자식이 Red, 오른쪽 자식이 Black인 경우
-> 형제노드를 Red로, 형제노드의 왼쪽 자식을 Black으로 칠한 후 형제노드를 기준으로 우회전 한다. 이후 케이스 4-c으로 처리
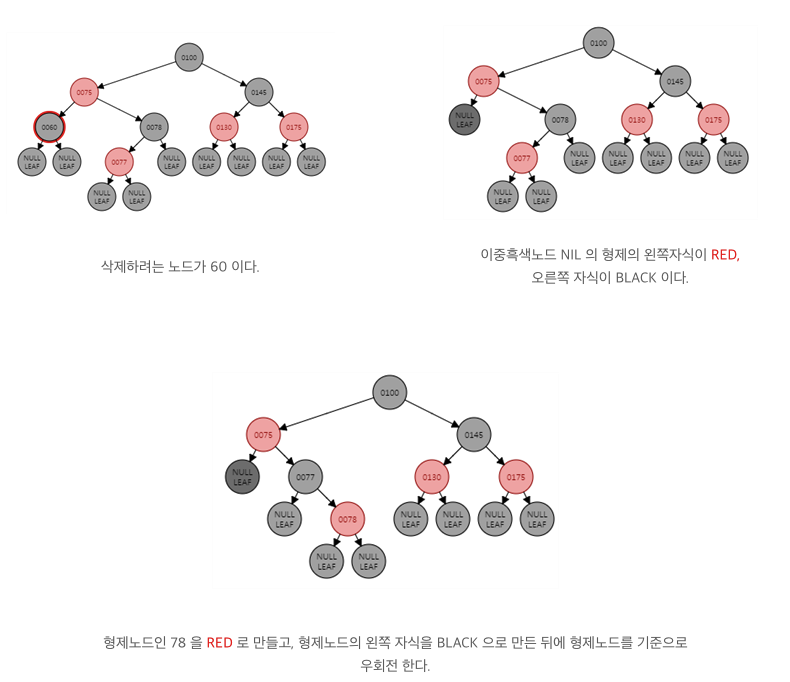
복잡한 케이스 4-c : 이중흑색노드의 형제가 Black이고 형제의 오른쪽 자식이 Red인 경우 (왼쪽은 no 상관)
-> 부모 노드의 색을 형제에게 넘긴다. 부모노드의 형제노드의 오른쪽 자식을 검은색으로 칠한다. 부모노드 기준으로 좌회전 한다.
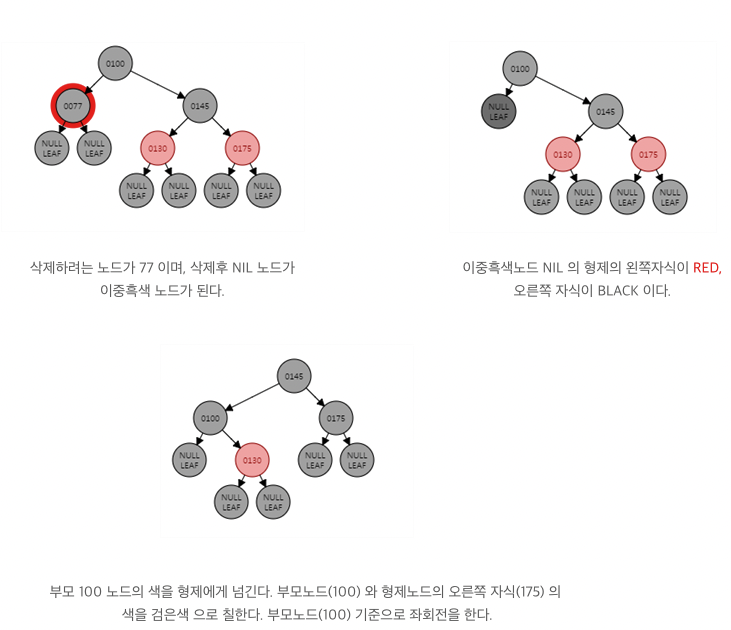
직접 정리한 내용 !
레드-블랙 트리 코드
위 내용은 이해를 위한 것이고 아래 코드는 위키피디아를 바탕으로 만들었다.
// 1. 노드는 레드 혹은 블랙 중의 하나이다.
// 2. 루트 노드는 블랙이다.
// 3. 모든 리프 노드들(NIL)은 블랙이다.
// 4. 레드 노드의 자식노드 양쪽은 언제나 모두 블랙이다. (즉, 레드 노드는 연달아 나타날 수
// 없으며,블랙 노드만이 레드 노드의 부모 노드가 될 수 있다)
// 5. 어떤 노드로부터 시작되어 그에 속한 하위 리프 노드에 도달하는 모든 경로에는 리프 노드를
// 제외하면 모두 same 개수의 블랙 노드가 있다.
#include "rbtree.h"
#include <malloc.h>
void delete_case1(rbtree* t, node_t *n);
void delete_case2(rbtree* t, node_t *n);
void delete_case3(rbtree* t, node_t *n);
void delete_case4(rbtree* t, node_t *n);
void delete_case5(rbtree* t, node_t *n);
void delete_case6(rbtree* t, node_t *n);
void delete_one_child(rbtree* t, node_t* n);
rbtree *new_rbtree(void) {
rbtree *p = (rbtree *)calloc(sizeof(rbtree), 1);
return p;
}
node_t *newNode(key_t k){
node_t *t = calloc(sizeof(node_t),1);
t->left = t->right = t->parent = NULL;
t->key = k;
t->color = RBTREE_RED; // RED
return t;
}
void delete_rbtree(rbtree *t) {
// TODO: reclaim the tree nodes's memory
free(t);
}
node_t *grandparent(node_t *t){
if ((t != NULL) && (t->parent != NULL)){
return t->parent->parent;
} else return NULL;
}
node_t *uncle(node_t *t){
node_t *g = grandparent(t);
if (g == NULL) return NULL; // no grandparent means no uncle
if (t->parent == g->left) return g->right;
else return g->left;
}
node_t *sibling(node_t *t){
if (t == t->parent->left)
return t->parent->right;
else
return t->parent->left;
}
void rotate_left(rbtree* t, node_t *n){ // 좌회전, 위 아래로 level이 바뀌는 노드 중 윗 노드가 들어와야함
node_t *cr = n->right; //
node_t *p = n->parent;
if (cr->left != NULL)
cr->left->parent = n;
n->right = cr->left;
n->parent = cr;
cr->left = n;
cr->parent = p;
if (p != NULL){
if (p->left == n)
p->left = cr;
else
p->right = cr;
}
else{t->root=cr;}
}
void rotate_right(rbtree* t, node_t *n){ // 우회전
node_t *cl = n->left; //
node_t *p = n->parent;
if (cl->right != NULL)
cl->right->parent = n;
n->left = cl->right;
n->parent = cl;
cl->right = n;
cl->parent = p;
if (p != NULL){
if (p->left == n)
p->left = cl;
else
p->right = cl;
}
else{t->root=cl;}
}
node_t *rbtree_insert(rbtree *t, const key_t key) {
// TODO: implement insert
node_t *new = newNode(key);
node_t *curr = NULL;
if (t->root == NULL){ // case 1 root== NULL
new->color = RBTREE_BLACK; // BLACK
t->root = new;
return t->root;
}
////////////////////////////////////////////////////////////////////
else{ // case 2,3,4,5 를 위해 새노드 위치 리프 노드까지 탐색
curr = t->root;
// t->root = curr;
while (curr != NULL){ // 노드 삽입 위치 찾기
if (curr->key < key){ // 새노드 key가 클 때
if(curr->right != NULL)
curr = curr->right;
else {// curr->right == NULL 일 때
curr->right = new;
new->parent = curr;
break;
}
}
else { // 새노드 key가 작을 때
if(curr->left != NULL)
curr = curr->left;
else {// curr->right == NULL 일 때
curr->left = new;
new->parent = curr;
break;
}
}
}
node_t* curr=new; // 이거 고침.. 다시 보기
while (1){ // case 1
if (curr->parent == NULL){
curr->color = RBTREE_BLACK;
return t->root;
}
//////////////////////////////////////////////////////////////////
else if (curr->parent->color == RBTREE_BLACK) // case 2 부모가 Black
return t->root; // 뭘 return 해야하지
//////////////////////////////////////////////////////////////////
else { // case 3 n, 부모, 삼촌이 Red => 부모, 삼촌 Black, 조부모 Red
node_t *u = uncle(curr), *g;
if ((u != NULL) && (u->color == RBTREE_RED)) { // 부모, 삼촌이 Red
curr->parent->color = RBTREE_BLACK; // 부모 Black
u->color = RBTREE_BLACK; // 삼촌 Black
g = grandparent(curr); // 조부모 생성
g->color = RBTREE_RED; // 조부모 Red
curr = g;
// curr = g;
continue;
}
// u : Black인 경우 빠져나옴
else{ // case 4 n : Red, p : Red, u : Black, g->left랑 p->right 처럼 반대 방향-> 좌회전
node_t *g = grandparent(curr);
if ((curr == curr->parent->right) && (curr->parent == g->left)){
rotate_left(t, curr->parent); // 위 아래로 level이 바뀌는 노드 중 위. 즉 parent가 아래로 내려가고 new가 올라감
curr = curr->left;
} else if ((curr == curr->parent->left)&& (curr->parent == g->right)){
rotate_right(t, curr->parent);
curr = curr->right;
}
g = grandparent(curr); // case 5
curr->parent->color = RBTREE_BLACK;
g->color = RBTREE_RED;
if (curr == curr->parent->left)
rotate_right(t, g);
else
rotate_left(t, g);
}
}
}
}
return t->root;
}
node_t *rbtree_find(const rbtree *t, const key_t key) {
node_t *curr = t->root;
while (1){
if (curr->key < key){ // key가 큼
if (curr->right != NULL) curr = curr->right;
else {return NULL;}
}
else if (curr->key > key){ // key가 작음
if(curr->left != NULL) curr = curr->left;
else {return NULL;}
}
else {return curr;}
}
return NULL;
}
node_t *rbtree_min(const rbtree *t) {
// TODO: implement find
node_t* n = t->root;
while(n->left != NULL)
n = n->left;
return n;
}
node_t *rbtree_max(const rbtree *t) {
// TODO: implement find
node_t* n = t->root;
while(n->right != NULL)
n = n->right;
return n;
}
/////////////////////////////////////////////////////////////////////////////////////////////////////
// 삭제 부분
int rbtree_erase(rbtree *t, node_t *p) { // p가 key값을 가진 node
// TODO: implement erase
if (t->root == NULL || p==NULL) return 0;
if (p->right != NULL && p->left != NULL){ // 삭제 노드 자식 2개
node_t* temp = p->left;
node_t* parent = NULL;
while(temp->right!=NULL){
parent=temp;
temp=temp->right;
}
if (parent!=NULL){
if(temp->left!=NULL){ // succesor의 부모노드
parent->right = temp->left;
temp->left->parent = parent; // 내가 추가
}
}
else{ // ???????????????
if (temp->left!=NULL){
p->left=temp->left;
}
}
p->key = temp->key;
delete_one_child(t,temp);
}
else{ // 삭제 노드 0개 or 1개
delete_one_child(t,p);
}
return 0;
}
void replace_node(node_t* t, node_t* child){
// 앞에서 n의 부모가 NULL이 되는 경우를 delete_case에 오지 않게 미리 처리해주면 된다.
child->parent = t->parent;
if(t->parent->left == t)
t->parent->left = child;
else if (t->parent->right == t)
t->parent->right = child;
}
void delete_one_child(rbtree* t, node_t *n) { // successor 자식 1개인 경우
/* 선제조건: n이 최대 하나의 non-null 자식을 갖고 있음.*/
if(t->root == n){
t->root=NULL;
free(n);
return;
}
if (n->left ==NULL && n->right == NULL){ // 자식이 없는 경우
if(n->color == RBTREE_BLACK){ // Red일 경우 바로 free
delete_case1(t, n);
}
if (n==n->parent->left){
n->parent->left = NULL;
}
else if(n==n->parent->right){
n->parent->right=NULL;
}
free(n);
return;
}
node_t *child; // 자식이 하나인 경우
if (n->left == NULL){
child = n->right;
}
else {
child = n->left;
}
replace_node(n, child);
if (n->color == RBTREE_BLACK) {
if (child->color == RBTREE_RED)
child->color = RBTREE_BLACK;
}
free(n);
}
void delete_case1(rbtree* t, node_t *n) // N이 root 일 때는 할 게 없음
{
if (n->parent != NULL)
delete_case2(t, n);
}
void delete_case2(rbtree* t, node_t *n) // S가 Red일 경우. P는 Black이고 S,P 색 바꾼 후 회전
{
node_t *s = sibling(n);
if (s->color == RBTREE_RED) {
n->parent->color = RBTREE_RED;
s->color = RBTREE_BLACK;
if (n == n->parent->left)
rotate_left(t, n->parent); // n이 개수가 적으므로 왼쪽에 있으면 좌회전
else
rotate_right(t, n->parent);
}
delete_case3(t, n);
}
void delete_case3(rbtree* t, node_t *n) // s, sl, sr이 모두 Black -> S를 Red -> 양쪽 same bH
{
node_t *s = sibling(n);
if ((n->parent->color == RBTREE_BLACK) &&
(s->color == RBTREE_BLACK) &&
(s->left->color == RBTREE_BLACK) &&
(s->right->color == RBTREE_BLACK)) {
s->color = RBTREE_RED;
delete_case1(t, n->parent); // 재귀 부분. p방향으로 올라가며 개수 하나씩 다 줄여줌
} else
delete_case4(t, n);
}
void delete_case4(rbtree* t, node_t *n) // p = Red, s, sr, sl = Black인 경우 p, s color swap. 왼쪽 BH +=1, 오른쪽 BH 유지
{
node_t *s = sibling(n);
if ((n->parent->color == RBTREE_RED) &&
(s->color == RBTREE_BLACK) &&
(s->left->color == RBTREE_BLACK) &&
(s->right->color == RBTREE_BLACK)) {
s->color = RBTREE_RED;
n->parent->color = RBTREE_BLACK;
} else
delete_case5(t, n);
}
void delete_case5(rbtree* t, node_t *n) // s, sr = Black, sl = Red 경우 sl, s 색 swap. s기준 우회전
{
node_t *s = sibling(n);
if (s->color == RBTREE_BLACK) {
/* 이 문은 자명하다,
case 2로 인해서(case 2에서 '''N'''의 형제 노드를 원래 형제 노드 '''S'''의 자식노드로 바꾸지만,
빨강 부모노드는 빨강 자식 노드를 가질 수 없기 때문에 '''N'''의 새로운 형제노드는 빨강일 수 없다). */
/* 다음의 문은 빨강을 '''N'''의 부모노드의 오른쪽 자식의 오른쪽 자식으로 두기 위함이다.
혹은 '''N'''의 부모노드의 왼쪽 자식의 왼쪽 자식으로 두기 위함. case 6에 넘기기 위해 */
if ((n == n->parent->left) &&
(s->right->color == RBTREE_BLACK) &&
(s->left->color == RBTREE_RED)) { /* this last test is trivial too due to cases 2-4. */
s->color = RBTREE_RED;
s->left->color = RBTREE_BLACK;
rotate_right(t, s);
} else if ((n == n->parent->right) &&
(s->left->color == RBTREE_BLACK) &&
(s->right->color == RBTREE_RED)) {/* this last test is trivial too due to cases 2-4. */
s->color = RBTREE_RED;
s->right->color = RBTREE_BLACK;
rotate_left(t, s);
}
}
delete_case6(t, n);
}
void delete_case6(rbtree* t, node_t *n) // 마지막 젤 빡센거. s = Black, sr = Red. // P색 -> s색, p, sr =-> Black p기준 좌회전
{
node_t *s = sibling(n); // s가 바뀌어서 새로 정의 해줘야 함
s->color = n->parent->color;
n->parent->color = RBTREE_BLACK;
if (n == n->parent->left) {
s->right->color = RBTREE_BLACK;
rotate_left(t, n->parent);
} else {
s->left->color = RBTREE_BLACK;
rotate_right(t, n->parent);
}
}
/////////////////////////////////////////////////////////////////////////////////////////////////////
int rbtree_to_array(const rbtree *t, key_t *arr, const size_t n) {
// TODO: implement to_array
return 0;
}
// 재귀를 이용한 출력 함수
void show(node_t *t) // 중위 순회 출력하는 함수
{
if (t == NULL){ // NULL인 경우 return
return;
}
if (t->left != NULL){
show(t->left);
}
printf("%d\n", t->key);
if (t->right != NULL){
show(t->right);
}
}
참조)
위키피디아 - 레드-블랙-트리
어스트락 - 레드블랙트리 - 삭제
'정글 2기 > 자료구조(C언어)' 카테고리의 다른 글
| [C언어] 이중포인터를 이용하여 배열을 교환하는 방법 (0) | 2021.09.14 |
|---|---|
| [C언어] 이진 탐색 트리(Binary Search Tree, BST) (0) | 2021.09.07 |
| [C언어] 연결 리스트(Linked list) 구현 (0) | 2021.09.05 |
| [C언어] 구조체 포인터 사용하기 (1) | 2021.09.04 |




댓글